The BurnMan Tutorial
Part 5: Equilibrium problems#
This file is part of BurnMan - a thermoelastic and thermodynamic toolkit for the Earth and Planetary Sciences
Copyright (C) 2012 - 2021 by the BurnMan team, released under the GNU GPL v2 or later.
Introduction#
This ipython notebook is the fifth in a series designed to introduce new users to the code structure and functionalities present in BurnMan.
Demonstrates
burnman.equilibrate, an experimental function that determines the bulk elemental composition, pressure, temperature, phase proportions and compositions of an assemblage subject to user-defined constraints.
Everything in BurnMan and in this tutorial is defined in SI units.
Phase equilibria#
What BurnMan does and doesn’t do#
Members of the BurnMan Team are often asked whether BurnMan does Gibbs energy minimization. The short answer to that is no, for three reasons: 1) Python is ill-suited to such computationally intensive problems. 2) There are many pieces of software already in the community that do Gibbs energy minimization, including but not limited to: PerpleX, HeFESTo, Theriak Domino, MELTS, ENKI, FactSAGE (proprietary), and MMA-EoS. 3) Gibbs minimization is a hard problem. The brute-force pseudocompound/simplex technique employed by Perple_X is the only globally robust method, but clever techniques have to be used to make the computations tractable, and the solution found is generally only a (very close) approximation to the true minimum assemblage. More refined Newton / higher order schemes (e.g. HeFESTo, MELTS, ENKI) provide an exact solution, but can get stuck in local minima or even fail to find a solution.
So, with those things in mind, what does BurnMan do? Well, because BurnMan can compute the Gibbs energy and analytical derivatives of composite materials, it is well suited to solving the equilibrium relations for fixed assemblages. This is done using the burnman.equilibrate function, which acts in a similar (but slightly more general) way to the THERMOCALC software developed by Tim Holland, Roger Powell and coworkers. Essentially, one chooses an assemblage (e.g. olivine + garnet +
orthopyroxene) and some equality constraints (typically related to bulk composition, pressure, temperature, entropy, volume, phase proportions or phase compositions) and the equilibrate function attempts to find the remaining unknowns that satisfy those constraints.
In a sense, then, the equilibrate function is simultaneously more powerful and more limited than Gibbs minimization techniques. It allows the user to investigate and plot metastable reactions, and quickly obtain answers to questions like “at what pressure does wadsleyite first become stable along a given isentrope?”. However, it is not designed to create P-T tables of equilibrium assemblages. If a user wishes to do this for a complex problem, we refer them to other existing codes. BurnMan
also contains a useful utility material called burnman.PerplexMaterial that is specifically designed to read in and interrogate P-T data from PerpleX.
There are a couple more caveats to bear in mind. Firstly, the equilibrate function is experimental and can certainly be improved. Equilibrium problems are highly nonlinear, and sometimes solvers struggle to find a solution. If you have a better, more robust way of solving these problems, we would love to hear from you! Secondly, the equilibrate function is not completely free from the curse of multiple roots - sometimes there is more than one solution to the equilibrium problem, and
BurnMan (and indeed any equilibrium software) may find one a metastable root.
Equilibrating at fixed bulk composition#
Fixed bulk composition problems are most similar to those asked by Gibbs minimization software like HeFESTo. Essentially, the only difference is that rather than allowing the assemblage to change to minimize the Gibbs energy, the assemblage is instead fixed.
In the following code block, we calculate the equilibrium assemblage of olivine, orthopyroxene and garnet for a mantle composition in the system NCFMAS at 10 GPa and 1500 K.
[1]:
import numpy as np
import matplotlib.pyplot as plt
import burnman
from burnman import equilibrate
from burnman.minerals import SLB_2011
# Set the pressure, temperature and composition
pressure = 3.e9
temperature = 1500.
composition = {'Na': 0.02, 'Fe': 0.2, 'Mg': 2.0, 'Si': 1.9,
'Ca': 0.2, 'Al': 0.4, 'O': 6.81}
# Create the assemblage
gt = SLB_2011.garnet()
ol = SLB_2011.mg_fe_olivine()
opx = SLB_2011.orthopyroxene()
assemblage = burnman.Composite(phases=[ol, opx, gt],
fractions=[0.7, 0.1, 0.2],
name='NCFMAS ol-opx-gt assemblage')
# The solver uses the current compositions of each solution as a starting guess,
# so we have to set them here
ol.set_composition([0.93, 0.07])
opx.set_composition([0.8, 0.1, 0.05, 0.05])
gt.set_composition([0.8, 0.1, 0.05, 0.03, 0.02])
equality_constraints = [('P', 10.e9), ('T', 1500.)]
sol, prm = equilibrate(composition, assemblage, equality_constraints)
print(f'It is {sol.success} that equilibrate was successful')
print(sol.assemblage)
# The total entropy of the assemblage is the molar entropy
# multiplied by the number of moles in the assemblage
entropy = sol.assemblage.S*sol.assemblage.n_moles
Warning: No module named 'cdd'. For full functionality of BurnMan, please install pycddlib.
It is True that equilibrate was successful
Composite: NCFMAS ol-opx-gt assemblage
P, T: 1e+10 Pa, 1500 K
Phase and endmember fractions:
olivine: 0.4971
Forsterite: 0.9339
Fayalite: 0.0661
orthopyroxene: 0.2925
Enstatite: 0.8640
Ferrosilite: 0.0687
Mg_Tschermaks: 0.0005
Ortho_Diopside: 0.0668
garnet: 0.2104
Pyrope: 0.4458
Almandine: 0.1239
Grossular: 0.2607
Mg_Majorite: 0.1258
Jd_Majorite: 0.0437
Each equality constraint can be a list of constraints, in which case equilibrate will loop over them. In the next code block we change the equality constraints to be a series of pressures which correspond to the total entropy obtained from the previous solve.
[2]:
equality_constraints = [('P', np.linspace(3.e9, 13.e9, 21)),
('S', entropy)]
sols, prm = equilibrate(composition, assemblage, equality_constraints)
The object sols is now a 1D list of solution objects. Each one of these contains an equilibrium assemblage object that can be interrogated for any properties:
[3]:
data = np.array([[sol.assemblage.pressure,
sol.assemblage.temperature,
sol.assemblage.p_wave_velocity,
sol.assemblage.shear_wave_velocity,
sol.assemblage.molar_fractions[0],
sol.assemblage.molar_fractions[1],
sol.assemblage.molar_fractions[2]]
for sol in sols if sol.success])
The next code block plots these properties.
[4]:
fig = plt.figure(figsize=(12, 4))
ax = [fig.add_subplot(1, 3, i) for i in range(1, 4)]
P, T, V_p, V_s = data.T[:4]
phase_proportions = data.T[4:]
ax[0].plot(P/1.e9, T)
ax[1].plot(P/1.e9, V_p/1.e3)
ax[1].plot(P/1.e9, V_s/1.e3)
for i in range(3):
ax[2].plot(P/1.e9, phase_proportions[i], label=sol.assemblage.phases[i].name)
for i in range(3):
ax[i].set_xlabel('Pressure (GPa)')
ax[0].set_ylabel('Temperature (K)')
ax[1].set_ylabel('Seismic velocities (km/s)')
ax[2].set_ylabel('Molar phase proportions')
ax[2].legend()
plt.show()
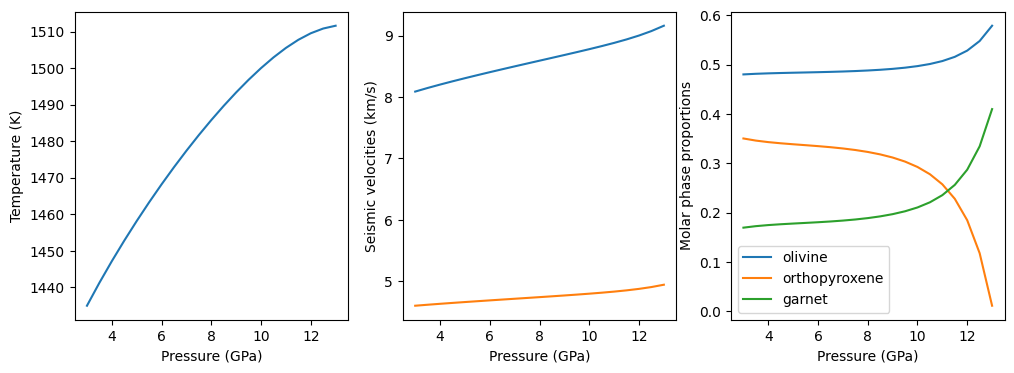
From the above figure, we can see that the proportion of orthopyroxene is decreasing rapidly and is exhausted near 13 GPa. In the next code block, we determine the exact pressure at which orthopyroxene is exhausted.
[5]:
equality_constraints = [('phase_fraction', [opx, 0.]),
('S', entropy)]
sol, prm = equilibrate(composition, assemblage, equality_constraints)
print(f'Orthopyroxene is exhausted from the assemblage at {sol.assemblage.pressure/1.e9:.2f} GPa, {sol.assemblage.temperature:.2f} K.')
Orthopyroxene is exhausted from the assemblage at 13.04 GPa, 1511.64 K.
Equilibrating while allowing bulk composition to vary#
[6]:
# Initialize the minerals we will use in this example.
ol = SLB_2011.mg_fe_olivine()
wad = SLB_2011.mg_fe_wadsleyite()
rw = SLB_2011.mg_fe_ringwoodite()
# Set the starting guess compositions for each of the solutions
ol.set_composition([0.90, 0.10])
wad.set_composition([0.90, 0.10])
rw.set_composition([0.80, 0.20])
First, we find the compositions of the three phases at the univariant.
[7]:
T = 1600.
composition = {'Fe': 0.2, 'Mg': 1.8, 'Si': 1.0, 'O': 4.0}
assemblage = burnman.Composite([ol, wad, rw], [1., 0., 0.])
equality_constraints = [('T', T),
('phase_fraction', (ol, 0.0)),
('phase_fraction', (rw, 0.0))]
free_compositional_vectors = [{'Mg': 1., 'Fe': -1.}]
sol, prm = equilibrate(composition, assemblage, equality_constraints,
free_compositional_vectors,
verbose=False)
if not sol.success:
raise Exception('Could not find solution for the univariant using '
'provided starting guesses.')
P_univariant = sol.assemblage.pressure
phase_names = [sol.assemblage.phases[i].name for i in range(3)]
x_fe_mbr = [sol.assemblage.phases[i].molar_fractions[1] for i in range(3)]
print(f'Univariant pressure at {T:.0f} K: {P_univariant/1.e9:.3f} GPa')
print('Fe2SiO4 concentrations at the univariant:')
for i in range(3):
print(f'{phase_names[i]}: {x_fe_mbr[i]:.2f}')
Univariant pressure at 1600 K: 12.002 GPa
Fe2SiO4 concentrations at the univariant:
olivine: 0.22
wadsleyite: 0.37
ringwoodite: 0.50
Now we solve for the stable sections of the three binary loops
[8]:
output = []
for (m1, m2, x_fe_m1) in [[ol, wad, np.linspace(x_fe_mbr[0], 0.001, 20)],
[ol, rw, np.linspace(x_fe_mbr[0], 0.999, 20)],
[wad, rw, np.linspace(x_fe_mbr[1], 0.001, 20)]]:
assemblage = burnman.Composite([m1, m2], [1., 0.])
# Reset the compositions of the two phases to have compositions
# close to those at the univariant point
m1.set_composition([1.-x_fe_mbr[1], x_fe_mbr[1]])
m2.set_composition([1.-x_fe_mbr[1], x_fe_mbr[1]])
# Also set the pressure and temperature
assemblage.set_state(P_univariant, T)
# Here our equality constraints are temperature,
# the phase fraction of the second phase,
# and we loop over the composition of the first phase.
equality_constraints = [('T', T),
('phase_composition',
(m1, [['Mg_A', 'Fe_A'],
[0., 1.], [1., 1.], x_fe_m1])),
('phase_fraction', (m2, 0.0))]
sols, prm = equilibrate(composition, assemblage,
equality_constraints,
free_compositional_vectors,
verbose=False)
# Process the solutions
out = np.array([[sol.assemblage.pressure,
sol.assemblage.phases[0].molar_fractions[1],
sol.assemblage.phases[1].molar_fractions[1]]
for sol in sols if sol.success])
output.append(out)
output = np.array(output)
Finally, we do some plotting
[9]:
fig = plt.figure()
ax = [fig.add_subplot(1, 1, 1)]
color='purple'
# Plot the line connecting the three phases
ax[0].plot([x_fe_mbr[0], x_fe_mbr[2]],
[P_univariant/1.e9, P_univariant/1.e9], color=color)
for i in range(3):
if i == 0:
ax[0].plot(output[i,:,1], output[i,:,0]/1.e9, color=color, label=f'{T} K')
else:
ax[0].plot(output[i,:,1], output[i,:,0]/1.e9, color=color)
ax[0].plot(output[i,:,2], output[i,:,0]/1.e9, color=color)
ax[0].fill_betweenx(output[i,:,0]/1.e9, output[i,:,1], output[i,:,2],
color=color, alpha=0.2)
ax[0].text(0.1, 6., 'olivine', horizontalalignment='left')
ax[0].text(0.015, 14.2, 'wadsleyite', horizontalalignment='left',
bbox=dict(facecolor='white',
edgecolor='white',
boxstyle='round,pad=0.2'))
ax[0].text(0.9, 15., 'ringwoodite', horizontalalignment='right')
ax[0].set_xlim(0., 1.)
ax[0].set_ylim(0.,20.)
ax[0].set_xlabel('p(Fe$_2$SiO$_4$)')
ax[0].set_ylabel('Pressure (GPa)')
ax[0].legend()
plt.show()
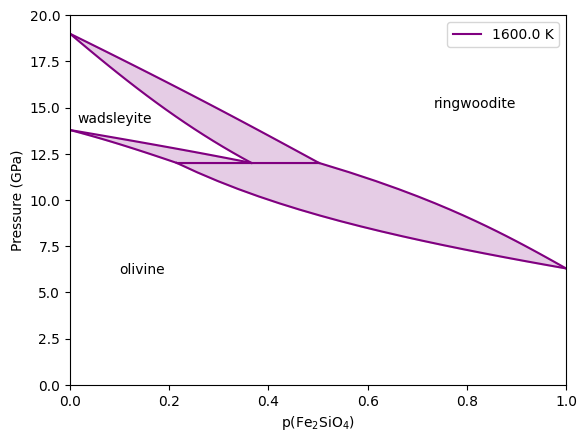
And we’re done!