The BurnMan Tutorial
Part 1: Material Classes#
This file is part of BurnMan - a thermoelastic and thermodynamic toolkit for the Earth and Planetary Sciences
Copyright (C) 2012 - 2021 by the BurnMan team, released under the GNU GPL v2 or later.
Introduction#
This ipython notebook is the first in a series designed to introduce new users to the code structure and functionalities present in BurnMan.
Demonstrates
burnman.Mineral: Equations of state, property modification schemes, initialization, interrogating properties at given pressure and temperature.
burnman.CombinedMineral: Initialization (otherwise similar to mineral).
burnman.Solution: Formulations (ideal, asymmetric, subregular), initialization, interrogating properties at given pressure, temperature and composition.
burnman.Composite: Initialization, interrogating properties at given pressure, temperature, phase proportions and using different seismic averaging schemes.
Everything in BurnMan and in this tutorial is defined in SI units.
Acknowledgments#
The authors are grateful to M. Ghiorso for useful discussions. R.M. would like to thank B. Watterson for the concept of Planet Zog (see Part 3: Layers and Planets).
This project was initiated at, and follow-up research support was received through, CIDER (NSF FESD grant 1135452). The development of BurnMan has been supported by the Computational Infrastructure for Geodynamics initiative (CIG), through the Science and Technologies Funding Council (U.K.) under Award No. ST/R001332/1 and through the Natural Environment Research Council (U.K.) Large Grant MC-squared (Award No. NE/T012633/1). The authors have also received support from the University of California - Davis.
Getting started with BurnMan#
Our first task is to import BurnMan. If you haven’t yet installed the current version, you can do this by typing pip install -e . from the top-level directory of the repository. Alternatively, you could just uncomment (remove the leading # from) the first line in the following code block. The second line in the code block imports the BurnMan module.
[1]:
#!pip install -q -e ..
import burnman
Warning: No module named 'cdd'. For full functionality of BurnMan, please install pycddlib.
Types of BurnMan Material objects#
The BurnMan package allows users to define and use objects that represent different kinds of Materials. The most important classes of Material are named Mineral, Solution and Composite. In the following subsections, we show how users can create objects of each type, set their state (pressure and temperature) and composition, and interrogate them for their material properties.
Mineral objects#
Mineral objects are the building blocks for more complex objects in BurnMan. These objects are intended to represent minerals (or melts, or fluids) of fixed composition, with a well-defined equation of state that defines the relationship between the current state (pressure and temperature) of the mineral and its thermodynamic potentials and derivatives (such as Gibbs energy, volume and entropy).
Mineral objects are initialized with a “params” dictionary containing all of the parameters required by the desired equation of state and an optional “property modifiers” argument. Here we initialize a generic Mineral, just to show the general structure:
[2]:
mineral_object = burnman.Mineral(params={}, property_modifiers=[[]])
The required keys in the parameters dictionary depends on the equation of state, described in the following section.
Equations of state#
BurnMan identifies the desired equation of state by checking the value of the string parameter “equation_of_state” in the parameters dictionary that is passed as an argument to the Mineral class. BurnMan currently contains implementations of the following static equations of state (i.e., equations of state with no temperature dependence): - “bm2”, “bm3” and “bm4”: Birch-Murnaghan (2nd, 3rd and 4th order) - “mt”: Modified Tait - “morse”: Morse potential - “vinet”: Vinet (originally the Rydberg equation of state) - “rkprime”: Reciprocal K-prime
And also the following thermal equations of state: - “mgd2” and “mgd3”: Mie-Debye-Grueneisen equation of state (second and third order expansions for the shear modulus) - “slb2” and “slb3”: Stixrude and Lithgow-Bertelloni (2011; second and third order expansions for the shear modulus) - “hp_tmt”: Thermal Modified Tait (Holland and Powell; 2011) - “dks_s”: de Koker and Stixrude (2013; solids) - “dks_l”: de Koker and Stixrude (2013; liquids) - “cork”: Compensated Redlich-Kwong equation of state - “aa”: Anderson and Ahrens (1998) - “brosh_calphad”: Brosh et al. (2007)
Each equation of state assumes the presence of a different set of keys in the “params” dictionary. These keys are checked and validated on initialization. Two important parameters for most mineral objects are the chemical formula of the mineral and its molar mass, which can be calculated using the functions “dictionarize_formula” and “formula_mass”.
[3]:
from burnman.tools.chemistry import dictionarize_formula, formula_mass
forsterite_formula = dictionarize_formula('Mg2SiO4')
molar_mass = formula_mass(forsterite_formula)
print(f'Formula in dictionary form: {forsterite_formula}')
print(f'Molar mass: {molar_mass:.5f} kg')
Formula in dictionary form: {'Mg': 2.0, 'Si': 1.0, 'O': 4.0}
Molar mass: 0.14069 kg
Below, we demonstrate the creation of a forsterite object for the Stixrude and Lithgow-Bertelloni (2011) equation of state which uses a 3rd order expansion for the shear modulus (equation_of_state = ‘slb3’).
[4]:
forsterite_params = {'name': 'Forsterite',
'formula': forsterite_formula,
'equation_of_state': 'slb3',
'F_0': -2055403.0,
'V_0': 4.3603e-05,
'K_0': 1.279555e+11,
'Kprime_0': 4.21796,
'Debye_0': 809.1703,
'grueneisen_0': 0.99282,
'q_0': 2.10672,
'G_0': 81.6e9,
'Gprime_0': 1.46257,
'eta_s_0': 2.29972,
'n': sum(forsterite_formula.values()),
'molar_mass': molar_mass}
forsterite = burnman.Mineral(params=forsterite_params)
print(forsterite.params)
{'name': 'Forsterite', 'formula': {'Mg': 2.0, 'Si': 1.0, 'O': 4.0}, 'equation_of_state': 'slb3', 'F_0': -2055403.0, 'V_0': 4.3603e-05, 'K_0': 127955500000.0, 'Kprime_0': 4.21796, 'Debye_0': 809.1703, 'grueneisen_0': 0.99282, 'q_0': 2.10672, 'G_0': 81600000000.0, 'Gprime_0': 1.46257, 'eta_s_0': 2.29972, 'n': 7.0, 'molar_mass': 0.14069310000000002, 'T_0': 300.0, 'E_0': 0.0, 'P_0': 0.0}
Property modifiers#
Thermodynamic models of minerals can include modifications to the properties predicted by the underlying equation of state. Often, this is done to approximate physical processes which were neglected during development of the equation of state.
BurnMan allows users to apply modifications to the Gibbs energy \(\mathcal{G}(P, T)\) via a “property_modifiers” attribute. This attribute takes the form of a list of different modifiers, which are themselves each composed of a list consisting of an identifying string and a dictionary containing the required parameters. The following modifiers are currently implemented in BurnMan: - “linear”: Linear in pressure and temperature (i.e. \(\Delta \mathcal{G} = \Delta \mathcal{E} - T \Delta S + P \Delta V\)) - “landau”: A Landau order-disorder transition (Putnis, 1992) - “landau_hp”: A Landau order-disorder transition (Holland and Powell, 2011) - “bragg_williams”: A Bragg-Williams order-disorder transition - “magnetic_chs”: A magnetic order-disorder transition
The following code block implements the Landau transition for hematite as given in the Holland et al. (2018) database (ds6.33).
[5]:
# Dictionary with parameters for equation of state.
hematite_params = {'name': 'hematite',
'formula': {'Fe': 2.0, 'O': 3.0},
'equation_of_state': 'hp_tmt',
'H_0': -825420.0,
'S_0': 87.4,
'V_0': 3.027e-05,
'Cp': [163.9, 0.0, -2257200.0, -657.6],
'a_0': 2.79e-05,
'K_0': 223000e6,
'Kprime_0': 4.04,
'Kdprime_0': -1.8e-11,
'n': 5.0,
'molar_mass': 0.1596882}
# Dictionary for Landau transition which modifieds the Gibbs energy
hematite_property_modifiers = [['landau_hp', {'P_0': 1.e5,
'T_0': 298.15,
'Tc_0': 955.0,
'S_D': 15.6,
'V_D': 0.0}]]
# Initialise mineral with a property modifier
hematite = burnman.Mineral(params=hematite_params,
property_modifiers=hematite_property_modifiers)
The CombinedMineral class#
In petrology, we are often interested in phases for which we have little experimental or theoretical information. One common example is when we want to approximate the properties of an ordered phase relative to its disordered counterparts. In many cases, a reasonable procedure is to make a mechanical mixture of the known phases, such that they are the correct composition of the unknown phase, and then apply a linear correction to the Gibbs energy of the phase (i.e. \(\Delta \mathcal{G} = \Delta \mathcal{E} - T \Delta S + P \Delta V\)). In BurnMan, we do this using the CombinedMineral class. In the lines below, we create an ordered orthopyroxene with composition MgFeSi\(_2\)O\(_6\) from a 50:50 mixture of enstatite and ferrosilite. We make this compound 6 kJ/mol more stable than the mechanical mixture.
[6]:
from burnman import CombinedMineral
from burnman.minerals import HP_2011_ds62
fe_mg_orthopyroxene = CombinedMineral(name='ordered ferroenstatite',
mineral_list=[HP_2011_ds62.en(),
HP_2011_ds62.fs()],
molar_amounts=[0.5, 0.5],
free_energy_adjustment=[-6.e3, 0., 0.])
print(fe_mg_orthopyroxene.formula)
Counter({'O': 6.0, 'Si': 2.0, 'Mg': 1.0, 'Fe': 1.0})
Implemented datasets#
BurnMan already includes several published mineral datasets. These can be found in the “minerals” subdirectory of BurnMan, and include the Stixrude and Lithgow-Bertelloni (2011) dataset, Holland et al. (2013) and Jennings et al. (2015) datasets. The script misc/table_mineral_library.py will list all minerals included for each equation of state.
Mineral objects can be initialised from these datasets using commands like the following:
[7]:
from burnman import minerals
fo_SLB = minerals.SLB_2011.forsterite()
fo_HP = minerals.HP_2011_ds62.fo()
The “()” at the end of each call indicate that these commands initialize an object from a class. This is done so that users can create multiple distinct objects with the same material parameters but potentially different states.
Interrogating the properties of a Mineral object at a given pressure and temperature#
Once an object has been initialised, the user can set its state (pressure in Pa and temperature in K):
[8]:
fo_SLB.set_state(1.e9, 1000)
The thermodynamic and seismic properties of the object at those conditions can then by returned as attributes of the object (returned in SI units):
[9]:
from burnman.tools.chemistry import formula_to_string
print(f'{fo_SLB.name} (SLB2011)')
print(f'Formula: {formula_to_string(fo_SLB.formula)}')
print(f'Gibbs: {fo_SLB.gibbs:.3e} J/mol')
print(f'S: {fo_SLB.molar_entropy:.3e} J/K/mol')
print(f'V_p: {fo_SLB.v_p:.3e} m/s')
Forsterite (SLB2011)
Formula: Mg2SiO4
Gibbs: -2.148e+06 J/mol
S: 2.747e+02 J/K/mol
V_p: 8.308e+03 m/s
It is common for users to want to return properties over a range of states. BurnMan makes this easy through the “evaluate” method of the Material class. In the following lines, we investigate the properties of quartz as defined by Stixrude and Lithgow Bertelloni (2011):
[10]:
# Necessary imports for creating the P, T arrays and plotting
import numpy as np
import matplotlib.pyplot as plt
# Temperatures and pressures at which to evaluate properties
temperatures = np.linspace(300., 1300., 1001)
pressures = 1.e5*np.ones_like(temperatures)
# Desired properties
properties = ['molar_heat_capacity_p', 'v_phi']
# Initialize a quartz object and print the parameters dictionary
# and property modifiers
qtz = minerals.SLB_2011.quartz()
print(qtz.params)
print(qtz.property_modifiers)
# Return arrays containing the desired properties
isobaric_heat_capacities, bulk_sound_velocities = qtz.evaluate(properties, pressures, temperatures)
# Plot the properties
fig = plt.figure(figsize=(8, 4))
fig.suptitle('Heat capacity and bulk sound velocity across alpha->beta transition in quartz')
ax = [fig.add_subplot(1, 2, i) for i in range(1, 3)]
ax[0].plot(temperatures, isobaric_heat_capacities)
ax[1].plot(temperatures, bulk_sound_velocities/1000.)
for i in range(2):
ax[i].set_xlabel('Temperature (K)')
ax[0].set_ylabel('Isobaric heat capacity (J/K/mol)')
ax[1].set_ylabel('Bulk sound velocity (km/s)')
ax[0].set_ylim(50., 150.)
ax[1].set_ylim(1.5, 5.)
fig.tight_layout()
fig.subplots_adjust(top=0.88)
{'name': 'Quartz', 'formula': {'Si': 1.0, 'O': 2.0}, 'equation_of_state': 'slb3', 'F_0': -858853.4, 'V_0': 2.367003e-05, 'K_0': 49547430000.0, 'Kprime_0': 4.33155, 'Debye_0': 816.3307, 'grueneisen_0': -0.00296, 'q_0': 1.0, 'G_0': 44856170000.0, 'Gprime_0': 0.95315, 'eta_s_0': 2.36469, 'n': 3.0, 'molar_mass': 0.0600843, 'T_0': 300.0, 'E_0': 0.0, 'P_0': 0.0}
[['landau', {'Tc_0': 847.0, 'S_D': 5.164, 'V_D': 1.222e-06}]]
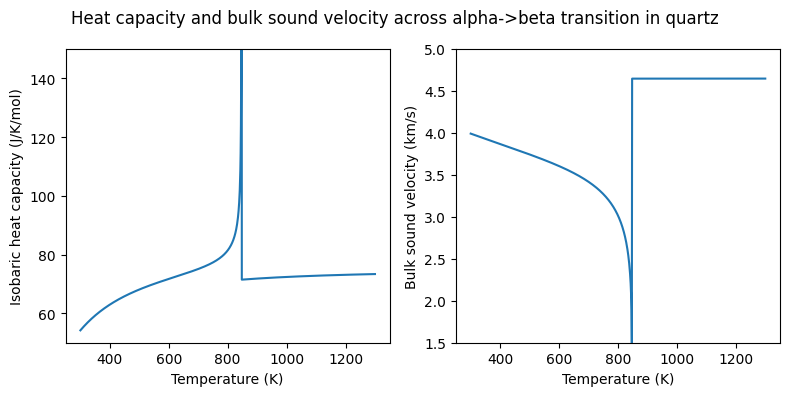
In the figure produced by the code above, one can see the effect of the alpha->beta transition in quartz (also known as the quartz inversion). This is a displacive transition from trigonal to hexagonal symmetry that can be modelled (as done here) by a Landau-type transition.
To give users confidence that BurnMan is outputting accurate derivative properties, we include a tool that checks the thermodynamic self-consistency of the equation of state:
[11]:
from burnman.tools.eos import check_eos_consistency
assert(check_eos_consistency(qtz, 1.e9, 1000., verbose=False))
Solution objects#
The Solution class in BurnMan allows users to define materials that have crystal chemical sites that can be occupied by multiple species. The species occupancies on the sites can be varied by changing the proportions of a number of ‘’independent’’ endmembers.
Currently, all the models implemented in BurnMan are of “Bragg-Williams” type (Bragg and Williams, 1930s). This means that the thermodynamic properties of solutions are uniquely defined by the average occupancies of species on each site (Myhill and Connolly, 2021). These models are therefore unable to accurately account for local interactions that give rise to short-range order, but Bragg-Williams models with multiple sites can provide a first-order approximation to the energetic effects of long-range order. From a microscopic standpoint, the distinction is an artificial one, since long-range order arises from local interactions (e.g. Bethe 1934, 1935). However, a detailed treatment of order-disorder requires either complex models (Kikuchi, 1951) or ab-initio simulations that have their own dedicated software packages (e.g. VASP).
Model formalisms#
The ideal model#
The simplest solution model implemented in BurnMan is the ideal solution model. In this solution, the excess Gibbs energy of mixing is purely configurational in nature. Mathematically:
\(\Delta \mathcal{G}^{\text{mix}} = -RT \sum_i m_i \sum_j p_{ij} \ln p_{ij}\)
where \(R\) is the gas constant (in J/K/mol), \(T\) is the temperature (in K), \(m_i\) is the multiplicity of site \(i\) and \(p_{ij}\) is the proportion of species \(j\) on site \(i\).
The following code initializes a binary ideal solution model between pyrope and almandine. The solution_model argument defines the solution model itself. The endmembers argument must be a list of lists containing all the endmembers of the solution. The first item in each inner list should contain a Mineral object corresponding to the endmember of interest. The second item should be a chemical formula. The exchange sites in this formula are denoted by square brackets, followed by the multiplicities \(m_i\) (optional if \(m_i = 1\)). Everything not contained within an “[…]m” block is ignored.
[12]:
from burnman import Solution, minerals
from burnman.classes.solutionmodel import IdealSolution
ideal_garnet = Solution(name = 'Ideal pyrope-almandine garnet',
solution_model = IdealSolution(endmembers = [[minerals.HP_2011_ds62.py(),
'[Mg]3[Al]2Si3O12'],
[minerals.HP_2011_ds62.alm(),
'[Fe]3[Al]2Si3O12']]
),
molar_fractions = [0.5, 0.5])
Each species on each site must begin with a capital letter, but the string does not have to correspond to an element. Partial occupancies are allowed. For example, [Al0.5Fef0.5] would be valid for an endmember with both \(\text{Al}^{3+}\) and \(\text{Fe}^{3+}\) on the same site. [Vac] would be valid for a vacancy, whereas [v] would not. The molar_fractions argument in the initialization above is optional.
As of BurnMan 1.1, ideality does not require that the multiplicity of each site is fixed between endmembers. This allows the implementation of Temkin-type models (Temkin, 1945), which are used to model melts. For example, here is the ideal part of the melt model proposed by Holland et al. (2018), restricted to the CMS system (nonideality and changes in endmember energies have been ignored):
[13]:
CMS_melt = Solution(name = 'CMAS melt (ideal approximation)',
solution_model = IdealSolution(endmembers = [[minerals.HGP_2018_ds633.q4L,
"[]0[Sinet]"],
[minerals.HGP_2018_ds633.wo1L,
"[Ca][Sichain]"],
[minerals.HGP_2018_ds633.fo2L,
"[Mg]4[Sitet]"]]
),
molar_fractions = [0.1, 0.4, 0.5])
In the endmember formulae above, the first site has different species (absent, Ca, Mg) and a different multiplicity (0, 1, 4) for the three endmembers. On the second site, the multiplicity is constant with composition, but Si is treated as three different species (network, chain and isolated tetrahedra).
The (a)symmetric model#
Another solution model formalism implemented in BurnMan is the asymmetric model (Holland and Powell, 2003). This model is an extension of the regular solution model (Wohl, 1946), with the extension following van Laar (1906).
The general idea is that there are interaction energies \(W_{ij}\) associated with each binary in the solution model. Those binary interactions are modified by a set of \(\alpha_k\) parameters, such that:
\(\Delta \mathcal{G}^{\text{mix}} = \Delta \mathcal{G}^{\text{mix,ideal}} + \Delta \mathcal{G}^{\text{mix,nonideal}}\)
and
\(\Delta \mathcal{G}^{\text{mix,nonideal}} = (\sum_l \alpha_l p_l) (\sum_i^{n-1} \sum_{j=i+1}^n \phi_i \phi_j \frac{2 w_{ij}}{\alpha_i + \alpha_j}\))
where
\(\phi_i = \frac{\alpha_i p_i}{\sum_k \alpha_k p_k}\)
\(\Delta \mathcal{G}^{\text{mix,ideal}}\) is caalculated using the same expressions as for the ideal model. The following code block initialises an asymmetric garnet model in the system CFMASO (taken from the Holland and Powell, 2011 dataset; ds6.2).
[14]:
from burnman.classes.solutionmodel import AsymmetricRegularSolution
g2 = Solution(name='asymmetric garnet (ThermoCalc ds6.2)',
solution_model=AsymmetricRegularSolution(endmembers=[[minerals.HP_2011_ds62.py(), '[Mg]3[Al]2Si3O12'],
[minerals.HP_2011_ds62.alm(), '[Fe]3[Al]2Si3O12'],
[minerals.HP_2011_ds62.gr(), '[Ca]3[Al]2Si3O12'],
[minerals.HP_2011_ds62.andr(), '[Ca]3[Fe]2Si3O12']],
alphas = [1.0, 1.0, 2.7, 2.7],
energy_interaction = [[2.5e3, 31.e3, 53.2e3],
[5.e3, 37.24e3],
[2.e3]]))
In the case that all \(\alpha_i\) are equal to each other, the asymmetric model becomes a symmetric model. BurnMan allows users to specify this type of model by setting solution_model=SymmetricRegularSolution(). In this case, the alphas argument does not need to be passed to SymmetricRegularSolution().
The subregular model#
BurnMan also contains an implementation of the subregular model (Helffrich and Wood, 1989). In this model, the excess nonideal Gibbs energy is expressed as a cubic polynomial in endmember proportions:
\(G^* = p_i G^{\text{mbr}}_i + p_i p_j W_{ij}^{\text{binary}} (1 + p_j - p_i)/2 + p_i p_j p_k W_{ijk}^{\text{ternary}}\)
where the binary terms must be equal to zero when \(i=j\) and the ternary terms can only be non-zero for \(i<j<k\).
[15]:
from burnman.classes.solutionmodel import SubregularSolution
# Parameters from Ganguly et al. (1996), converted to SI units
Wh_1bar = [[[2117., 695.], [9834., 21627.], [12083., 12083.]],
[[6773., 873.], [539., 539.]],
[[0., 0.]]]
Wv = [[[0.07e-5, 0.], [0.058e-5, 0.012e-5], [0.04e-5, 0.03e-5]],
[[0.03e-5, 0.], [0.04e-5, 0.01e-5]],
[[0., 0.]]]
Ws = [[[0., 0.], [5.78, 5.78], [7.67, 7.67]],
[[1.69, 1.69], [0., 0.]],
[[0., 0.]]]
# We now convert from 1 bar enthalpy, entropy and volume (1 cation basis)
# to energy, entropy and volume (3 cation basis)
mult = lambda x, n: [[[v*n for v in i] for i in j] for j in x]
add = lambda x, y: [[[x[i][j][k] + y[i][j][k] for k in range(len(x[i][j]))]
for j in range(len(x[i]))] for i in range(len(x))]
energy_interaction = add(mult(Wh_1bar, 3.), mult(Wv, -3.e5))
volume_interaction = mult(Wv, 3.)
entropy_interaction = mult(Ws, 3.)
g3 = Solution(name='CFMnMAS garnet (Ganguly et al., 1996)',
solution_model=SubregularSolution(
endmembers=[[minerals.HP_2011_ds62.py(), '[Mg]3[Al]2Si3O12'],
[minerals.HP_2011_ds62.alm(), '[Fe]3[Al]2Si3O12'],
[minerals.HP_2011_ds62.gr(), '[Ca]3[Al]2Si3O12'],
[minerals.HP_2011_ds62.spss(), '[Mn]3[Al]2Si3O12']],
energy_interaction=energy_interaction,
volume_interaction=volume_interaction,
entropy_interaction=entropy_interaction,
energy_ternary_terms = [[0, 1, 2, 0.e3]],
volume_ternary_terms = [[0, 1, 2, 0.e-6]],
entropy_ternary_terms = [[0, 1, 2, 0.]]))
For the model above, the ternary terms are all equal to zero, but in general, the structure of the ternary_terms input is a list of lists, where the inner list corresponds to the three endmember indices \(i<j<k\) followed by the value of the interaction term.
Implemented datasets#
As for the endmembers, BurnMan already contains solution models from multiple datasets. One of these is the Stixrude and Lithgow-Bertelloni (2011) dataset. In the code-block below, we initialize an object using the three-endmember (FMAS) bridgmanite solution from that publication.
[16]:
bdg = minerals.SLB_2011.mg_fe_bridgmanite()
bdg.endmembers
[16]:
[[<burnman.minerals.SLB_2011.mg_perovskite at 0x7f4eb72aa350>, '[Mg][Si]O3'],
[<burnman.minerals.SLB_2011.fe_perovskite at 0x7f4eb749bd10>, '[Fe][Si]O3'],
[<burnman.minerals.SLB_2011.al_perovskite at 0x7f4eb73c41d0>, '[Al][Al]O3']]
Interrogating the properties of a Solution object at a given composition, pressure and temperature#
Unlike Minerals, Solutions can vary in composition. Before interrogating properties, it is therefore necessary to set both the state (using the method “set_state”) and the composition (using the method “set_composition”).
[17]:
bdg.set_composition([0.8, 0.1, 0.1])
bdg.set_state(30.e9, 2000.)
print(f'Bridgmanite composition: {dict(bdg.formula)}')
print(f'Bridgmanite volume: {bdg.V:.3e} m')
print(f'Bridgmanite endmember partial Gibbs energies:')
for pG in bdg.partial_gibbs:
print(f' {pG/1e3:.3e} kJ/mol')
Bridgmanite composition: {'Mg': 0.8, 'Si': 0.9, 'O': 3.0, 'Fe': 0.1, 'Al': 0.2}
Bridgmanite volume: 2.315e-05 m
Bridgmanite endmember partial Gibbs energies:
-9.690e+02 kJ/mol
-6.868e+02 kJ/mol
-1.143e+03 kJ/mol
The evaluate method can be used to output properties of solutions at constant composition:
[18]:
pressures = np.linspace(30.e9, 130.e9, 101)
temperatures = 2000.*np.ones_like(pressures)
densities, p_wave_velocities = bdg.evaluate(['rho', 'v_p'], pressures, temperatures)
# The following lines do the plotting
fig = plt.figure(figsize=(8, 4))
ax = [fig.add_subplot(1, 2, i) for i in range(1, 3)]
ax[0].plot(pressures/1.e9, densities)
ax[1].plot(pressures/1.e9, p_wave_velocities/1000.)
for i in range(2):
ax[i].set_xlabel('Pressure (GPa)')
ax[0].set_ylabel('Densities (kg/m^3)')
ax[1].set_ylabel('P wave velocity (km/s)')
fig.tight_layout()
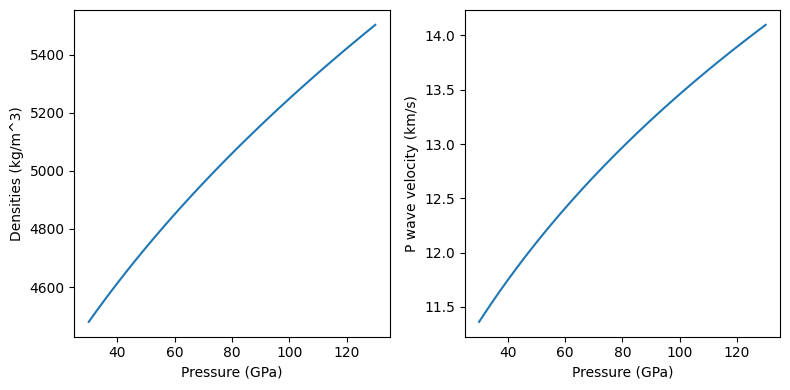
The “set_composition” method must be used every time the Solution composition is to be changed:
[19]:
import numpy as np
import matplotlib.pyplot as plt
comp = np.linspace(1e-5, 1.-1e-5, 101)
bdg_excess_gibbs_400 = np.empty_like(comp)
bdg_excess_gibbs_800 = np.empty_like(comp)
bdg_excess_gibbs_1200 = np.empty_like(comp)
bdg_activities_400 = np.empty((101, 3))
bdg_activities_800 = np.empty((101, 3))
bdg_activities_1200 = np.empty((101, 3))
pressure = 1.e9
for i, c in enumerate(comp):
molar_fractions = [1.0 - c, c, 0.]
bdg.set_composition(molar_fractions)
bdg.set_state(pressure, 400.)
bdg_excess_gibbs_400[i] = bdg.excess_gibbs
bdg_activities_400[i] = bdg.activities
bdg.set_state(pressure, 800.)
bdg_excess_gibbs_800[i] = bdg.excess_gibbs
bdg_activities_800[i] = bdg.activities
bdg.set_state(pressure, 1200.)
bdg_excess_gibbs_1200[i] = bdg.excess_gibbs
bdg_activities_1200[i] = bdg.activities
fig = plt.figure(figsize=(8, 4))
ax = [fig.add_subplot(1, 2, i) for i in range(1, 3)]
ax[0].plot(comp, bdg_excess_gibbs_400/1000., 'r-', linewidth=1., label='400 K')
ax[0].plot(comp, bdg_excess_gibbs_800/1000., 'g-', linewidth=1., label='800 K')
ax[0].plot(comp, bdg_excess_gibbs_1200/1000., 'b-', linewidth=1., label='1200 K')
ax[1].plot(comp, bdg_activities_1200[:,0], 'b-', linewidth=1., label='MgSiO$_3$')
ax[1].plot(comp, bdg_activities_1200[:,1], 'b:', linewidth=1., label='FeSiO$_3$')
ax[0].set_title("MgSiO$_3$-FeSiO$_3$ bridgmanite join")
ax[0].set_ylabel("Excess gibbs free energy of solution (kJ/mol)")
ax[1].set_ylabel("Endmember activities")
for i in range(2):
ax[i].set_xlabel("Molar FeSiO$_3$ fraction")
ax[i].legend(loc='lower left')
fig.tight_layout()
plt.show()
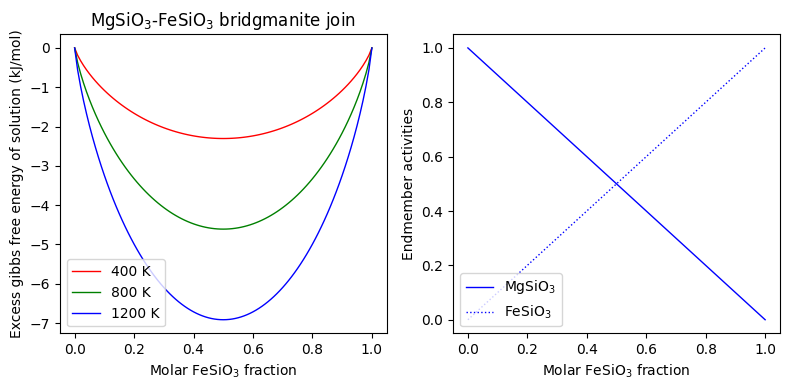
Composite objects#
The third major class derived from Material is the Composite class. This class is designed to represent collections of other Materials, which are typically objects of type Mineral and Solution, but can be any Material, including other Composites. A list of Materials is passed to the argument “phases” on initialization of a Composite object.
The properties of Composite materials can be interrogated in a similar manner to Solutions. To set the molar fractions of the material, either pass an array of fractions as the argument “fractions” on initialization, or use the “set_fractions” method at any time after initialization. As before, “set_state” is used to set the pressure and temperature of the object.
[20]:
from burnman import Composite
bdg = minerals.SLB_2011.mg_fe_bridgmanite()
fper = minerals.SLB_2011.ferropericlase()
bdg.set_composition([0.9, 0.1, 0.0])
fper.set_composition([0.8, 0.2])
assemblage = Composite(phases=[bdg, fper],
fractions=[0.5, 0.5],
fraction_type='molar',
name='rock')
pressure = 30.e9
temperature = 2000.
assemblage.set_fractions([0.5, 0.5])
assemblage.set_state(pressure, temperature)
print(f'Assemblage density at {pressure/1.e9} GPa and {temperature} K: {assemblage.density:.1f} kg/m^3')
Assemblage density at 30.0 GPa and 2000.0 K: 4491.0 kg/m^3
As for the Solution class, the properties of Composites at fixed phase fraction and phase compositions can be obtined using the evaluate method of the class. In the following code block, we evaluate the seismic properties of our 50:50 molar mixture of bridgmanite and ferropericlase from 30 to 130 GPa at 2000 K.
In this code block, we also demonstrate the ability for BurnMan to switch between different schemes for averaging seismic properties. Available schemes are “Voigt”, “Reuss”, “VoigtReussHill” (the standard scheme, which averages the Voigt and Reuss averages), “HashinShtrikmanLower” and “HashinShtrikmanUpper”. The figure shows the difference between the Reuss (lower) and Voigt (upper) bounds on the P-wave and S-wave velocities.
[21]:
pressures = np.linspace(30.e9, 130.e9, 101)
temperatures = np.ones(101)*2000.
assemblage.set_averaging_scheme('VoigtReussHill')
densities, Vp_VRH, Vs_VRH = assemblage.evaluate(['rho', 'v_p', 'v_s'],
pressures, temperatures)
assemblage.set_averaging_scheme('Reuss')
Vp_R, Vs_R = assemblage.evaluate(['v_p', 'v_s'], pressures, temperatures)
assemblage.set_averaging_scheme('Voigt')
Vp_V, Vs_V = assemblage.evaluate(['v_p', 'v_s'], pressures, temperatures)
fig = plt.figure(figsize=(8, 4))
ax = [fig.add_subplot(1, 2, i) for i in range(1, 3)]
ax[0].plot(pressures/1.e9, densities)
ax[1].fill_between(pressures/1.e9, Vp_R/1.e3, Vp_V/1.e3, alpha=0.2)
ax[1].fill_between(pressures/1.e9, Vs_R/1.e3, Vs_V/1.e3, alpha=0.2)
ax[1].plot(pressures/1.e9, Vs_R/1.e3, color='orange', linewidth=0.5)
ax[1].plot(pressures/1.e9, Vs_V/1.e3, color='orange', linewidth=0.5, label='$V_S$')
ax[1].plot(pressures/1.e9, Vp_R/1.e3, color='blue', linewidth=0.5)
ax[1].plot(pressures/1.e9, Vp_V/1.e3, color='blue', linewidth=0.5, label='$V_P$')
for i in range(2):
ax[i].set_xlabel('Pressure (GPa)')
ax[0].set_ylabel('Density (kg/m$3$)')
ax[1].set_ylabel('Velocities (km/s)')
fig.tight_layout()
plt.show()
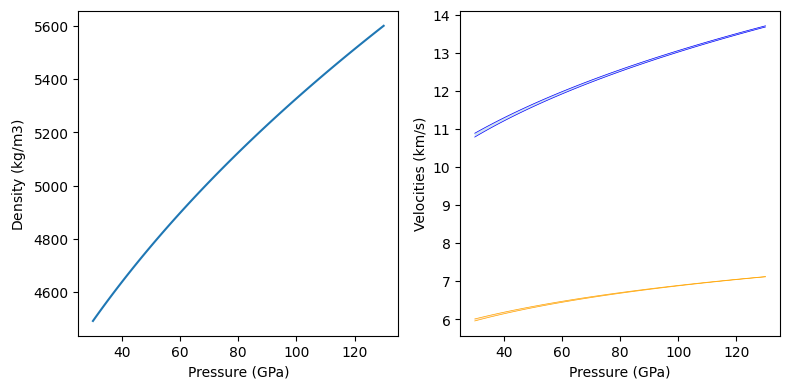
In the next part of the tutorial, we will look at BurnMan’s Composition class.